A Comprehensive Guide on How To Solve the Quadratic Equation 4x^2 – 5x – 12 = 0.
Learn the step-by-step process to solve the quadratic equation 4x^2 – 5x – 12 = 0 in this comprehensive guide. Understand the techniques and methods to find the solutions.

Solving quadratic equations can sometimes feel like navigating a maze, especially when faced with complex coefficients and variables. This article delves into the intricacies of solving the quadratic equation 4x^2 – 5x – 12 = 0. We’ll break down the process into manageable steps, providing insights and tips to make the journey easier. By the end of this guide, you’ll have a clear understanding of how to approach and successfully solve this quadratic equation.
How To Solve This 4x^2 – 5x – 12 = 0?
To solve the quadratic equation 4x^2 – 5x – 12 = 0, follow these steps:
Step 1: Understand the Quadratic Equation
Before diving into the solution, it’s essential to understand the nature of the quadratic equation. A quadratic equation is a second-degree polynomial equation that can be written in the form ax^2 + bx + c = 0, where “a,” “b,” and “c” are coefficients. In our equation, a = 4, b = -5, and c = -12.
Step 2: Factorization
One of the primary methods to solve quadratic equations is through factorization. We need to find two numbers whose product is “a * c” (4 * -12 = -48) and whose sum is “b” (-5). These numbers are -8 and 3. Now, rewrite the middle term (-5x) as the sum of these two numbers: -8x + 3x.
Step 3: Set Up Equations
Split the equation 4x^2 – 5x – 12 = 0 into two separate equations:
- 4x^2 – 8x + 3x – 12 = 0
- 4x(x – 2) + 3(x – 4) = 0
Step 4: Solve for x
Set each factor equal to zero and solve for “x”:
- 4x = 0 –> x = 0
- x – 2 = 0 –> x = 2
- x – 4 = 0 –> x = 4
So, the solutions for the equation 4x^2 – 5x – 12 = 0 are x = 0, x = 2, and x = 4.
Mastering Quadratic Equations
Solving Quadratic Equations: Strategies Beyond Factorization
While factorization is an effective method for solving many quadratic equations, there are instances where it might not be the most suitable approach. In such cases, alternative methods like completing the square or using the quadratic formula come into play. These methods offer a broader toolkit for tackling various types of quadratic equations.
Completing the Square: Unveiling the Hidden Form
Completing the square is a technique that transforms a quadratic equation into a perfect square trinomial. It involves manipulating the equation to express it in the form (x – p)^2 = q, where “p” and “q” are constants. This method is particularly useful when dealing with quadratic equations that don’t easily factor.
The Quadratic Formula: A Universal Solution
The quadratic formula is a powerful tool that can solve any quadratic equation, regardless of its coefficients. The formula states that for an equation ax^2 + bx + c = 0, the solutions for “x” are given by the formula:
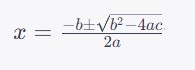
Common FAQs
Q: Is factorization the only way to solve quadratic equations?
A: No, while factorization is a commonly used method, there are alternatives like completing the square and the quadratic formula.
Q: Can quadratic equations have more than two solutions?
A: Quadratic equations can have at most two distinct solutions. In some cases, the solutions may be repeated.
Q: What if the coefficient “a” is equal to zero?
A: If the coefficient “a” is zero, the equation becomes linear, not quadratic. Linear equations have a single solution.
Q: Are the solutions for the equation unique?
A: Yes, the solutions are unique for a given quadratic equation. However, different quadratic equations can have the same solutions.
Q: How do quadratic equations relate to real-life problems?
A: Quadratic equations are often used to model various real-world scenarios, such as projectile motion or financial analysis.
Q: Can complex numbers be solutions to quadratic equations?
A: Yes, quadratic equations can have complex solutions when the discriminant (b^2 – 4ac) is negative.
Conclusion
Solving the quadratic equation 4x^2 – 5x – 12 = 0 might initially seem like a daunting task, but armed with the right techniques and methods, it becomes an achievable feat. Whether you opt for factorization, completing the square, or the quadratic formula, each approach brings you closer to uncovering the solutions. Remember, quadratic equations are not just abstract mathematical concepts; they have real-world applications and implications. Mastering the art of solving quadratics opens doors to understanding and solving various problems across different domains.
